学习排列组合问题的关键是:先要非常明确一些基本模型,这些基本模型往往只用很小的数字就能说明,然后再做一些数字大的问题就思路清晰了。
概念
排列
所谓排列组合,排列在组合之前,咱们要聊的第一个概念是“排列”,排列的英文是 Permutation 或者 Arrangement,因此在数学符号中,用 P 或者 A 表示都可以,二者意思完全一样。
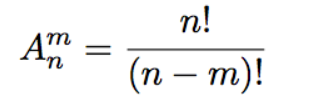
常见的 P (或 A) 右边会跟两个数字(或字母),右下角的数字 n 表示总数,
右上角的数字 m 表示抽出的个数。整个符号的意思是“从 n 个人中,
有顺序地抽出 m 个人的抽法数”,可以读作“P n 抽 m”。
那么,到底什么叫做有顺序的?我们来举个数字很小的例子:
例如:班里有三名同学,成绩前两名有几种可能性?
从3个数中选出2个数有A(3,2)=3!/(3-2)!=6 ,有6种可能性
组合
第二个概念是“组合”,它比排列更常用,组合的英文是 Combination,因此在数学符号中用 C 表示,美国和英国教材中,也常用“长括号”表示组合数。
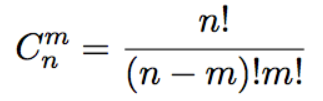
常见的 C 右边会跟两个数字(或字母),右下角的数字 n 表示总数,
右上角的数字 m 表示抽出的个数。整个符号的意思是“从 n 个人中,
不计顺序地抽出 m 个人的抽法数”,可以读作“C n 抽 m”。
那么,到底什么叫做不计顺序的?我们也来举个例子:
例如:班里有三名同学,选出两名代表参加年级会议有几种选法?
从3个数中选出2个数有C(3,2)=3!/(3-2)!2!=3 ,有3种选法
组合与排列的区别
与顺序有关的为排列问题,与顺序无关的为组合问题
捆绑法
排列组合中的相邻问题可以通过捆绑法来解决。
捆绑法的基本思路是,将要求相邻的元素视为一个整体(即一个“大元素”),然后与其他元素一起进行排列。同时,需要注意这个“大元素”内部元素的排列
具体步骤如下:
将要求相邻的元素捆绑在一起,视为一个整体。
将这个整体与其他元素一起进行全排列。
考虑这个整体内部元素的排列。由于它们是相邻的,所以需要考虑它们之间的相对顺序。
例题分析
例题1
5个男生和3个女生排成一排,3个女生必须排在一起,有多少种不同排法?( )
A. 240 B. 320 C. 450 D. 4320
答案 D
分析
3个女生必须在一起,采用捆绑法,把3个女生捆绑在一起当作一个元素
第1步
把3个女生视为一个元素,与5个男生进行排列,共有 A(6,6)=6 * 5 * 4 * 3 *2 * 1=720
第2步
3个女生内部再进行排列,A(3,3) = 3 * 2 * 1=6
需要2步完成,需采用乘法原理对2步排列数进行相乘:720 * 6 = 4320种
例题2
用数字0、1、2、3、4组成没有重复的五位数,其中数字1,2相邻的偶数有( )种
A. 16 B. 24 C. 32 D. 48
答案 B
分析
数字1,2相邻,采用捆绑法,把1,2捆绑起来当作一个元素
由于组成的5位数是偶数,所以末尾数字是0,2,4,而0不能在首位,2必须和1在一起所以要分类讨论
- 末尾数字是0
第1步
1,2捆绑在一起,和3,4各1个数字,组成3个元素,进行全排列 A(3,3) = 3 * 2 * 1 =6
第2步
捆绑的1,2内部进行排列 A(2,2)=2
分步根据乘法原理 6 * 2 =12 种
- 末尾数字是2
第1步
末尾数字是2,其中1和2捆绑在一起,所以4和5位置对应是1和2,是1种
第2步
还剩3个位置,第1个位置比较特殊,不能放0,所以只能在3和4中选1个,C(2,1)=2
第3步
还剩下2个位置2和3,没用其他限制,放入剩余的2个数字 A(2,2)=2
分步完成,根据乘法原理 1 * 2 * 2=4
- 末尾数字是4
第1步
末尾数字是4,是1种
第2步
其中1和2捆绑在一起,看做一个元素,所以还剩3个元素(0,1和2,3),安排到对应3个位置上
0不能做首位,所以首位只能从剩下2个元素中选1个 C(2,1)=2
第3步
还剩下2元素需要安排到2个位置上 A(2,2) =2
第4步
捆绑的1,2内部进行排列 A(2,2)=2
分步完成,根据乘法原理 1 * 2 * 2 *2 = 8
综上,末尾作为0,2,4三种情况分类讨论,故根据加法原理计算总数
所以 12 + 4 + 8 = 24 种
插板法
插板法一般用来解决求分解一定数量的无差别物体的方法的总数,使用插板法一般有三个要求:
①)所要分解的物体一般是相同的:
②所要分解的物体必须全部分完:
③参与分物体的组至少都分到1个物体,不能有没分到物体的组出现,
例题分析
例题1
10个相同的苹果分给4个小朋友,每个小朋友至少分1个,则有几种分法?
解析:这个题目就是典型的插板法模型题,题目满足三个条件,所以可直接用插板法,10个苹果9个间隔,可任意选择3个间隔插入挡板分隔成4份。C(9,3)=84
例题2:
某单位订阅了30份学习材料发放给3个部门,每个部门至少发放9份材料。问一共有多少种不同的发放方法?
解析:此题不满足“插板法”的条件是至少9份。而不是至少1份。采取“还原”思路,先给这几个部门都先发放8个,则剩30-8×3=6份。这时候每个部门就至少还需1份了。对剩下的6份分给3个部门运用插板法,即6份学习材料5个间隔,可任意选择2个间隔插入挡板分隔成3份。即C(5,2)=10
例题3:
12个相同的苹果装到编号为1,2,3 的三个不同盒子里面,则有多少种装法?
解析:此题不满足的条件是缺少至少1个。也当于是至少0个。根据我们上述的分析,采取“还原”思路,先给三个盒子各提供1个给总数,这样使得三个盒子就满足至少1个苹果的要求了。因此总数就变为12+3=15个。对15个的苹果运用插板法,即15个苹果14个间隔,可任意选择2个间隔插入挡板分隔成3份,C(14,2)=91
插空法
插空法就是先将其他元素排好,再将所指定的不相邻的元素插入到他们的间隙或两端位置,从而解决问题的策略,运用插空法解答有关元素不相邻的问题非常方便。
插空法的解题思路 ①:先排其他元素 ②再插空不相邻的元素
例题解析
例题1:
有4盒不同红花和3盘相同的白花排一排,有多少种不同的排法?
A.120 B.240 C.360 D.180
【答案】B。解析:先将不同的红花先排,有A44种排法,然后将相同的白花插入到4盘红花中,有5个空,因为花一样,不考虑排序,有C53种插法,由乘法原理得A44xC53等于240。
例题2:
有4盒不同红花和3盘不同的白花排一排,有多少种不同的排法?
A. 240 B. 480 C. 720 D.1440
【答案】D。解析:先将不同的红花先排,有A44种排法,然后将不同的白花插入到4盘红花中,有5个空,因为花不相同,考虑排序,有A53种插法,由乘法原理得A44xA53等于1440。
例题3:
学校安排一天的课程,有4节不同的理论课,3节不同实训课,2节不同活动课制定课表,要求实训课排一起,活动课不相邻的排法有几种?
A.1680 B.21800 C.21600 D.28600
【答案】C。解析:可将3节实训课捆绑在一起当做1个元素,但是有内部排序A33,将4节理论课和实训课看成5个元素先排,A55种方法,5个元素中有6个空,将2节实训课插入到6个空中,A62种插空法,一共有A55×A33×A62种方法,等于21600。
例题4:
学校安排一天的课程,有4节不同的理论课,3节不同实训课,2节不同活动课制定课表,要求最后结束的是活动课且活动课不相邻的排法有几种?
A.60560 B.34580 C.21600 D.70560
【答案】D。解析:可将1节活动课放在右侧先固定,有A21种排法,将4节不同的理论课和3节不同实训课共7节课排在左边,有A77种排法,接下来将剩下的1节活动课插在左边的7个空中既不与最后的活动课相邻,共有A21×A77×A71种,等于70560。
例题5:
学校安排一天的课程,有4节不同的理论课,3节相同实训课,2节不同活动课制定课表,要求最后结束的是活动课且活动课不相邻的排法有几种?
A.1200 B.1600 C.1800 D.2000
【答案】A。解析:可将1节活动课放在右侧先固定,有A21种排法,将4节不同的理论课和3节相同实训课共5个元素排在左边,有A55种排法,接下来将剩下的1节活动课插在左边的5个空中既不与最后的活动课相邻,共有A21×A55×A51种,1200种。
排列组合问题,历年初赛题集:
1、(CSP-J 2023)小明在某一天中依次有七个空闲时间段,他想要选出至少一个空闲时间段来练习唱歌,但他希望任意两个练习的时间段之间都有至少两个空闲的时间段让他休息。则小明一共有( B )种选择时间段的方案。
A. 31 B. 18 C. 21 D. 33
题解:
选一个空闲时段练歌有:7种 选两个空闲时间段练歌有:而且每个之间要有两个空闲时段,所以是C(5,2)=10种 选三个空闲时间段练歌有:1种 所以共有7+10+1=18种,答案 B
2、(CSP-J 2021)6 个人,两个人组一队,总共组成三队,不区分队伍的编号。不同的组队情况有( B )种。
A. 10 B. 15 C. 30 D. 20
题解:
本题要求在6人中两人一组进行组队,共组成三队,则:
对于第一支队伍:此时有6人可选,有C(6,2)=15 种组合
对于第二支队伍:此时有4人可选,有C(4,2)=6 种组合
对于第三支队伍:此时仅剩2人可选,只有1种组合
所以共有1561=90种不同组合。
题目中要求不区分队伍的编号(这里可以假设6人编号分别为A,B,C,D,E,F),那么组合中相同队伍的情况会出现6次。
例如:组队组合是AB一队,CD一队,EF一队
那么AB,CD,EF AB,EF,CD CD,AB,EF CD,EF,AB EF,AB,CD EF,CD,AB这6种组合,按照题目的要求都被视为同一种组队情况。
所以不区分队伍的编号,不同的组队情况有90/6=15种
正确答案应该选B。
3、(CSP-J 2020)5 个小朋友并排站成一列,其中有两个小朋友是双胞胎,如果要求这两个双胞胎必须相邻,则有( A )种不同排列方法?
A. 48 B. 36 C. 24 D. 72
题解:
两个双胞胎由于必须站一起,所以将他们看作一个人,则将排队看作4个人无顺序排,再乘上2个双胞胎的站列情况,即为 A(4,4)A(2,2)=4!2!=432121=242=48 答案 A
4、(CSP-J 2020)10 个三好学生名额分配到 7 个班级,每个班级至少有一个名额,一共有( A )种不同的分配方案。
A. 84 B. 72 C. 56 D. 504
题解:
使用插板法,10个名额可以插入九个,7个班级插入6个板子就可以实现,C(9,6)=84 选A
(CSP-J 2019)把8个同样的球放在5个同样的袋子里,允许有的袋子空着,共有( )种不同的分法。(提示:如果8个球都放在一个袋子里,无论是哪个袋子,都只算一种分法。) A.22 B.24 C.18 D.20
题解:
把问题合成,先思索5个袋子都不空的状况,再思索4个袋子不空的状况,以此类推,最后思索只运用一个袋子的状况(这种分法只要1种),把一切子状况的分法数相加求出总分法。
进一步剖析,运用k个袋子装n个球(袋子不空),一共有几种分法的问题能够转化为k个数相加等于n的种数问题。
运用5个袋子装8个球则有3种:
1+1+1+1+4 = 8
1+1+1+2+3 = 8
1+1+2+2+2 = 8
运用4个袋子分8个球则有5种:
1+1+1+5=8
1+1+2+4=8
1+1+3+3=8
1+2+2+3=8
2+2+2+2=8
运用3个袋子分8个球则有5种:
1+1+6=8
1+2+5=8
1+3+4=8
2+2+4=8
2+3+3=8
运用2个袋子分8个球则有4种:
1+7=8
2+6=8
3+5=8
4+4=8
运用1个袋子装8个球则有1种:
8=8
因而,该问题的答案即为一切子状况下的和,3+5+5+4+1 = 18。