一、算法的时间复杂度
什么是算法的时间复杂度呢?
即执行算法所需要的计算工作量。
那么如何衡量一个算法的时间复杂度呢?
直接把程序运行一遍,用系统时间或者执行次数来衡量嘛?这样做比较容易受运行环境的影响,在性能高的机器上跑出来的结果与在性能较低的机器上跑出来的结果相差很大。而且对测试时使用的数据规模也有很大的关系。
那怎么衡量呢?
——大O表示法
即T(n) = O(f(n))
【f(n)表示每行代码执行次数之和,而O表示正比例关系,这个公式的全称是:算法的渐进时间复杂度。】
先看个例子
#include<bits/stdc++.h>
using namespace std;
int main() {
int j=0;
for(int i=1;i<=n;i++)
{
j=i;
j++;
}
return 0;
}
通过「 大O符号表示法 」,这段代码的时间复杂度为:O(n),即这段代码在最坏情况下执行的次数接近n次。
【算法复杂度可以从最理想情况、平均情况和最坏情况三个角度来评估,由于平均情况大多和最坏情况持平,而且评估最坏情况也可以避免后顾之忧,因此一般情况下,我们设计算法时都要直接估算最坏情况的复杂度。】
大O表示法具体如何表示呢?
比如某个算法的时间复杂度如下,其中n代表数据量。
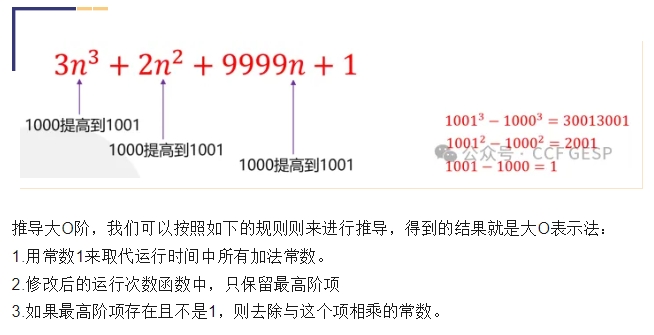
二、常见的时间复杂度
常见的时间复杂度量级有:
常数阶O(1)
对数阶O(logn)
线性阶O(n)
线性对数阶O(nlogn)
平方阶O(n^2)
立方阶O(n^3)
K次方阶O(n^k)
指数阶O(2^n)
阶乘阶O(n!)
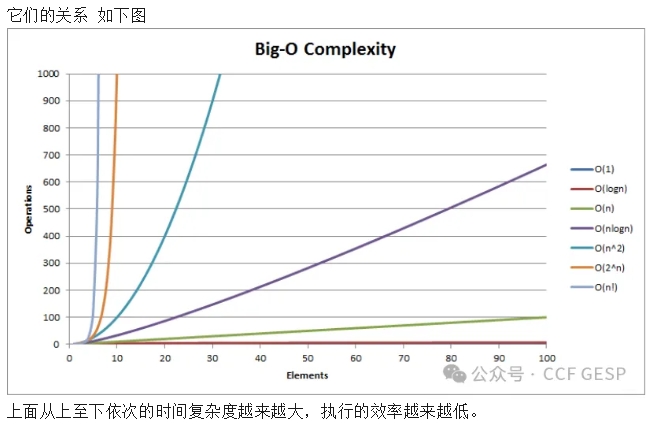
常见时间复杂度代码演示
常数阶O(1):无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1)
int i = 1;
int j = 2;
j++;
int m=i + j;
线性阶o(n):这个在最开始的代码示例中就讲解过了,如下面这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度
for(i=1;i<=n;i++)
{
j=i;
j++;
}
对数阶o(logN):这个在最开始的代码示例中就讲解过了,从下面代码可以看到,在whil循环里面,每次都将ⅰ乘以2,乘完之后,i距离n就越来越近了。我们试着求解一下,假设循环x次之后就大于2了,此时这个循环就退出了,也就是说2的x次方等阶,也就是说当循环log2^n次以后,这个代码就结束,这个代码的时间复杂度为:O(logn)
int i=1;
while(i<n)
{
i=i*2;
}
线性对数阶o(nlogN): 其实非常容易理解,将时间复杂度为o(logn)的代码循环N遍的话,那么它的时间复杂度就是o(nlongN)
for(m=1;m>n;m++)
{
i=1;
while(i<n)
{
i =i*2;
}
}
平方阶0(n^2)就更容易理解了,如果把 O(n)的代码再嵌套循环一遍,它的时间复杂度就是 O(n^2)了。
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
x=j;
x++;
}
}
常见数据结构的算法的时间复杂度分析
数组:数组的访问时间复杂度为O(1),插入和删除操作的时间复杂度通常为O(n)。空间复杂度方面,数组占用连续的内存空间,大小为n的数组空间复杂度为O(n)。
链表:链表的访问时间复杂度为O(n),插入和删除操作的时间复杂度可以为O(1)(在已知节点位置的情况下)。空间复杂度方面,链表每个节点占用一定的空间,总空间复杂度与节点数量成正比,即O(n)。
栈和队列:栈和队列的访问、插入和删除操作的时间复杂度通常为O(1)(在已知操作位置的情况下)。空间复杂度方面,它们占用连续的内存空间,大小与元素数量成正比,即O(n)。
排序算法:不同的排序算法具有不同的时间复杂度和空间复杂度。例如,冒泡排序和插入排序的时间复杂度为O(n^2),空间复杂度为O(1);快速排序的时间复杂度平均为O(nlogn),最坏情况下为O(n^2),空间复杂度通常为O(logn)(递归调用栈所需空间);归并排序的时间复杂度稳定为O(nlogn),但空间复杂度为O(n)(需要额外的存储空间进行归并操作)。