背包问题 —— 01背包

背包问题指在规定背包容量为m的前提下，每个物品对应的体积为v[i]，价值为w[i]，从物品0到物品i中选择物品放入背包中，找出符合某种要求的价值。 背包问题的本质上是一个选择问题，即通过选择来得到最大价值或各种各样的性质。

动态规划基础知识

DP 问题我们一般的思路是先确定解法的基本形式，再在它的基础上做优化。

首先我们对DP问题的分析流程做一下定义， 对于DP问题我们要确定的要素主要为

(1) 状态表示 ：dp 元素表示的是哪个集合

（以01背包问题为例： (i, j) 代表了只考虑在 1~i 范围内选择物品，并且体积小于等于 j 的所有状态的集合） 存的数是表示集合的哪一个属性（目标）

（以01背包问题为例：dp(i, j) 代表了(i, j)代表的所有状态集合中最大价值） 动态规划一般包含（MIN, MAX, COUNT）三种目标。

(2) 状态计算（状态转移方程）：对应的是集合的划分，如何将当前的集合dp( i,j )划分成几个更小的子集。

01背包：指每种物品只能选择1个。

二维动态规划

了解了这些以后我们就可以基于这个思路对01背包问题做一些分析：

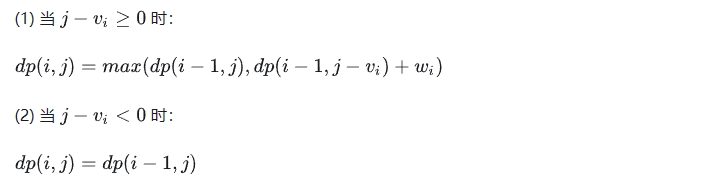
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int dp[N][N];
int m,n;
int main(){
    cin>>m>>n;
    int v[N],w[N];
    for(int i=1;i<=n;i++){
        cin>>v[i]>>w[i]; 
    }
     //?01背包：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]) 
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            // 当前物品重量大于背包容量时，不放该物品
            if(j < v[i]) dp[i][j] = dp[i - 1][j];
            // 当前物品重量小于等于背包容量时，在放该物品后和不放该物品之间选择一个最大价值
            else  dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
        }
    }    
    cout << dp[n][m] << endl; 
    return 0;
}

状态压缩 : 一维动态规划

dp问题的所有优化都是在代码上做等价变形 ， 和问题本身无关，只和代码逻辑有关。 01背包在时间复杂度上没法再优化， 从空间上我们其实还能做一些优化。

1、首先其实可以发现整个转移方程中对于 i 这一维，只用到了i -1， 所以我们其实并不需要记录所有的dp[i][..]，相反只需要用单个变量记录即可（滚动数组）。这样我们可以得出 2、在去除dp 数组的 i 这一维后，我们碰到了一些问题：对于 j 这一维因为 j - v[i] < j , 所以实际上 dp[j-v[i]] 这个状态已经被计算过了，这代表了什么呢，每次循环开始时 dp[j] 记录的是dp[i-1][j]的信息，而循环结束更新后 dp[j] 记录的则为dp[i][j]的信息，如果我们从前往后循环，那么我们每次更新时dp[j] = dp[j - v[i]]+w[i] 相当于原先二维动态规划时的 dp[i][j] = dp[i][j-v[i]]+w[i], 然而实际的目标 为 dp[i][j] = dp[i-1][j-v[i]]+w[i]， 那么怎么去修正这一点呢？ 我们从大到小循环， 这样则保证了每一次的 i 都是由 i - 1 推出来的 （dp[j-v[i]]在本轮尚未更新过，所以依旧记录的是dp[i-1][j-v[i]]的数值）。

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int dp[N];
//一维数组的解法 
int main(){ 
    int n, m;
    int v[N], w[N]; 
    cin >> m >> n;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i]; 
    for(int i = 1; i <= n; i++) {
        // 从后向前遍历，表示装入一个物品后，剩余的可装入容量达到的最大价值
        for(int j = m; j >= v[i]; j--) {
        	//dp[j]表示容量为j的背包，所背的物品价值最大为dp[j] 
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    } 
    cout << dp[m] << endl; 
    return 0;
}