什么是动态规划？
动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
动态规划核心思想
动态规划最核心的思想，就在于拆分子问题，记住过往，减少重复计算。 一个网上很流行的例子，帮助我们来更好的了解动态规划
A ： "1+1+1+1+1+1+1+1 =？"
A ： "上面等式的值是多少"
B ： 计算 "8"
A : 在上面等式的左边写上 "1+" 呢？
A : "此时等式的值为多少"
B : 很快得出答案 "9"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"
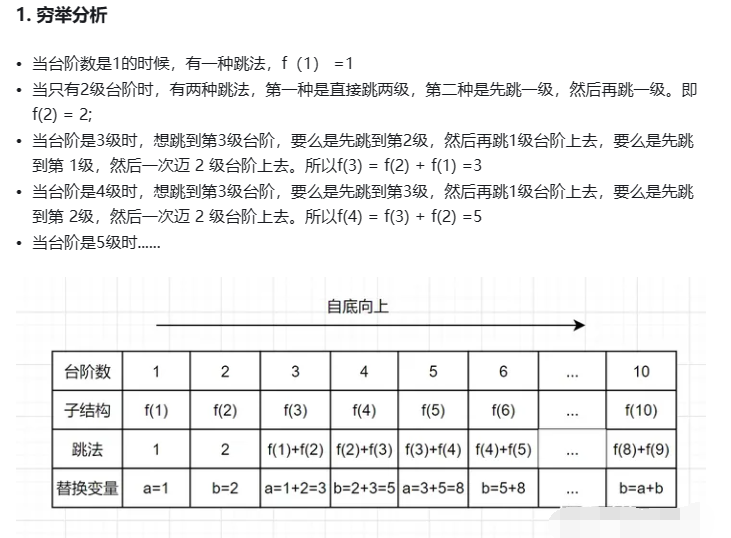
青蛙跳阶问题
大家第一次见这个题的时候，可能会有点蒙圈，不知道怎么解决。其实可以试想：
★
要想跳到第10级台阶，要么是先跳到第9级，然后再跳1级台阶上去;要么是先跳到第8级，然后一次迈2级台阶上去。
同理，要想跳到第9级台阶，要么是先跳到第8级，然后再跳1级台阶上去;要么是先跳到第7级，然后一次迈2级台阶上去。
要想跳到第8级台阶，要么是先跳到第7级，然后再跳1级台阶上去;要么是先跳到第6级，然后一次迈2级台阶上去。
”
假设跳到第n级台阶的跳数我们定义为f(n)，很显然就可以得出以下公式：
f（10） = f（9）+f(8)
f (9) = f(8) + f(7)
f (8) = f(7) + f(6)
...
f(3) = f(2) + f(1)
即通用公式为: f(n) = f(n-1) + f(n-2)
那f(2) 或者 f(1) 等于多少呢？
当只有2级台阶时，有两种跳法，第一种是直接跳两级，第二种是先跳一级，然后再跳一级。即f(2) = 2;
当只有1级台阶时，只有一种跳法，即f（1）= 1；
暴力递归解法
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1e9+7;
int f(int n){
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
return f(n-1) + f(n-2);
}
int main()
{
int n;
cin>>n;
cout<<f(n)%MOD;
return 0;
}
上面的解法，当输入的台阶数比较多时，就会出现超时，无法计算出结果。这是因为，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n)，就是指数级别的，爆炸增长的，如果n比较大的话，超时就很正常了。
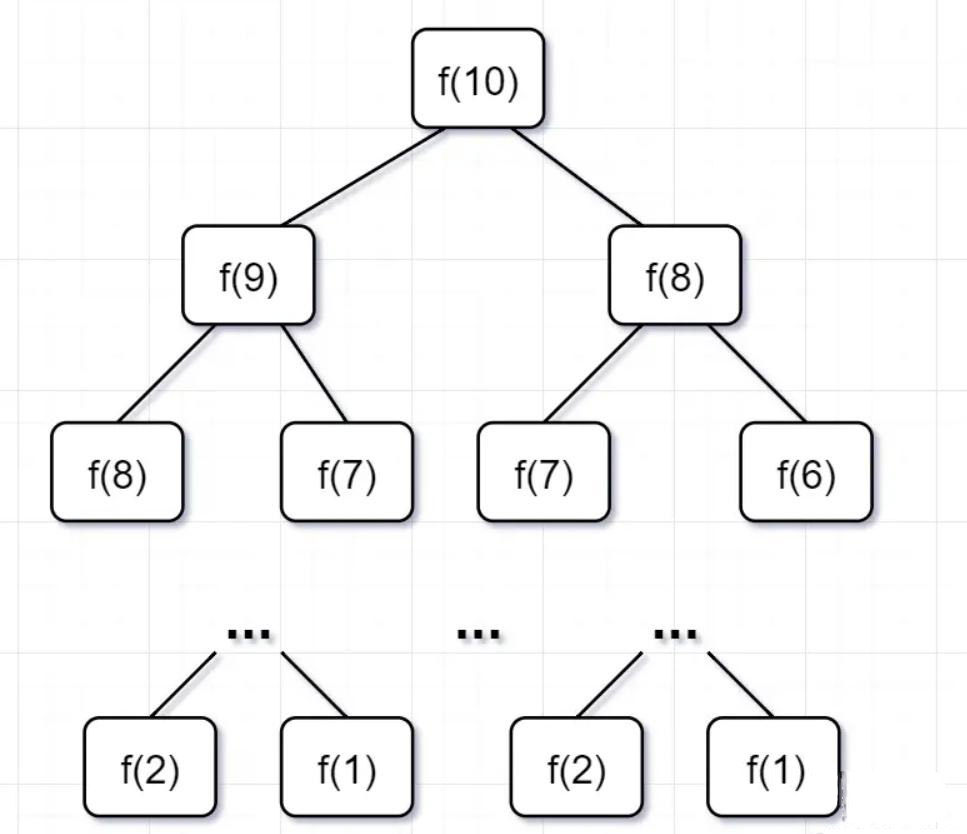查看上面的递归树，会发现存在大量重复计算，比如f（8）被计算了两次，f（7）被重复计算了3次...所以这个递归算法低效的原因，就是存在大量的重复计算！既然存在大量重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去备忘录查一下，如果有，就直接取就好了，备忘录没有才开始计算，那就可以省去重新重复计算的耗时啦！这就是动态规划的解法。
自底向上的动态规划
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1e9+7;
int f(int n){
if (n<= 1)
{
return 1;
}
if (n == 2)
{
return 2;
}
int a = 1;
int b = 2;
int temp = 0;
for (int i = 3; i <= n; i++) {
temp = (a + b)% MOD;
a = b;
b = temp;
}
return temp;
}
int main()
{
int n;
cin>>n;
cout<<f(n);
return 0;
}
什么样的问题可以考虑使用动态规划解决呢？
如果一个问题，可以把所有可能的答案穷举出来，并且穷举出来后，发现存在重叠子问题，就可以考虑使用动态规划。 比如一些求最值的场景，如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等，都是动态规划的经典应用场景。
动态规划的解题思路
动态规划的核心思想就是拆分子问题，记住过往，减少重复计算。 并且动态规划一般都是自底向上的，因此到这里，基于青蛙跳阶问题，我总结了一下我做动态规划的思路：
穷举分析 确定边界 找出规律，确定最优子结构 写出状态转移方程
